郑州外国语学校调研这几个选填纯属堆结论,尤其第8题!

.第  题的核心在于系数和是定值，这个可以用定比点差法证明，把 , 分别用  表示就可以。计算出定值，用 ,, 的式子表示以后，剩下的就是解一个基础的关于  的不等式即可！

郑州外国语学校2026届高三上学期调研5·8

.已知椭圆  的左、右焦点分别为 ,, 点 ,, 都在椭圆上, 若 ,, 且 , 则椭圆  的离心率的取值范围为 ....

被硬塞进来的结论： 其实是定值

用定比点差证：

设 ，，

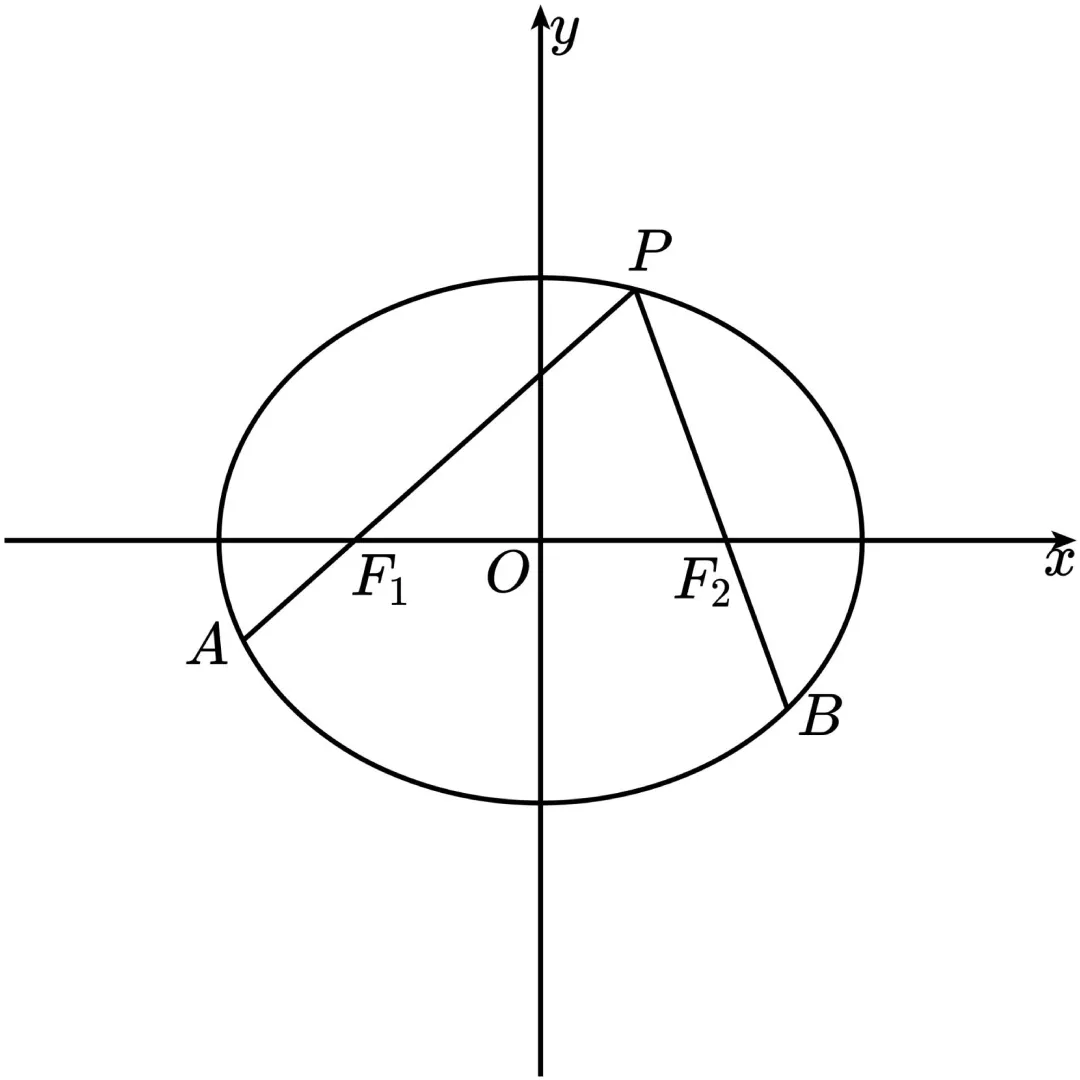
又 

同理 

.第  题其实主要看的还是轨迹思想，到原点距离为  的点轨迹当然是单位圆，说明啥呢，单位圆和这个已知的圆相交，我们用圆与圆相交搞定它就可以！

郑州外国语学校2026届高三上学期调研5·13

.已知动圆  上总存在不同的两点 , 到坐标原点的距离都等于 , 则实数  的取值范围是 .

到坐标原点  距离为  的点轨迹为：

 与圆  相交

.第  题主要是难算，但是仍然是普通的。首先先列关于零点的俩方程，然后两个式子相除，接下来比值换元反解  和 ，都用含  的式子表达。然后复合函数，先拿下  的范围，得到 ，再一个 ，利用算出范围即可拿下！

郑州外国语学校2026届高三上学期调研5·14

.已知函数 ,．设函数 , 若  有两个不同的零点 ,, 且 , 则  的取值范围为 .

即  有两个不同零点 

则 ，

记 ，则 

则 ，

以下令 

则 

从而 

进一步得：

令 

则 

则