郑州外国语高二期末考试难题讲解

.关于求导中三次函数的问题。我们需要知道一个结论，三次函数要想有  个零点，必须要极大值大于 ，极小值小于 。如果是有  个和  个零点，会发现都不满足题意！

24-25高二上·江苏泰州·期末

.已知函数  既有极大值又有极小值, 则实数  的取值范围是 ....

令 ,

令  得  或 

令  得 

 在 

图象如下：

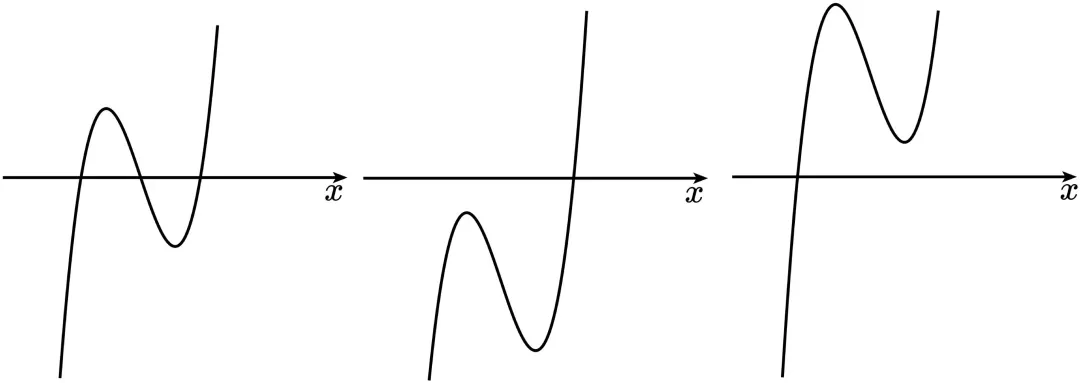
要想同时有极大值、极小值

则 

.旋转的双曲线。法一就是模仿正常的双曲线找实轴虚轴焦距的办法来类比找旋转的双曲线，逻辑是先找实轴端点再根据  来计算  值，法二比较直接，发起坐标系旋转一步到位！当然，这里的推理我们是按照三角函数的逻辑进行的推理！

25-26高二上·安徽·月考

.某数学兴趣小组研究发现：奇函数  的图象是双曲线, 如图, 该双曲线有两条渐近线. 若以该双曲线的中心为原点, 两个焦点所在直线为  轴重新建立直角坐标系, 则此时双曲线的标准方程为 .

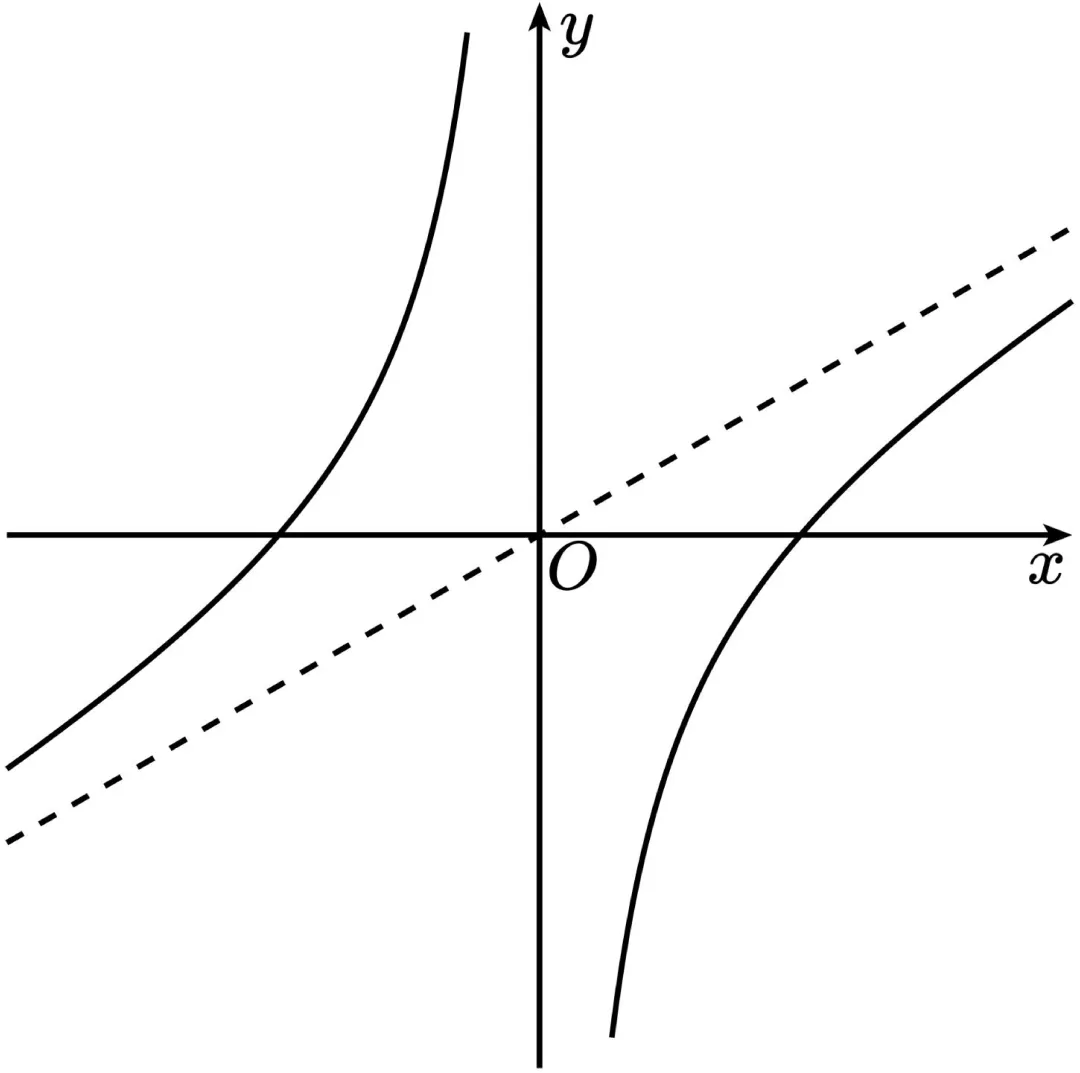
其实就是坐标系发生了旋转：

法一：

则 

则  及  是两条渐近线

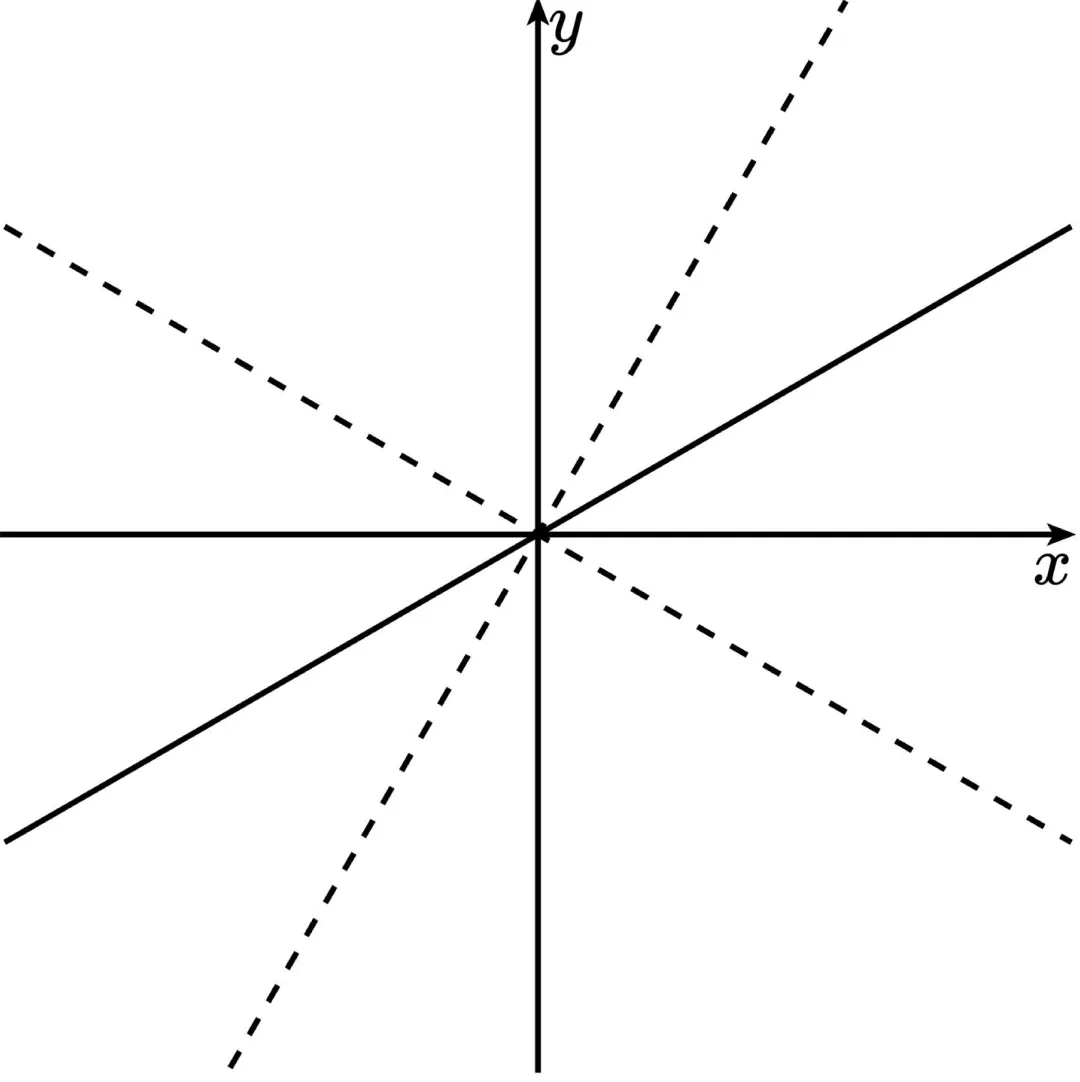
则  是虚轴

 为实轴

则 

由 ，则 

则两个交点为 

，

则重新建系后

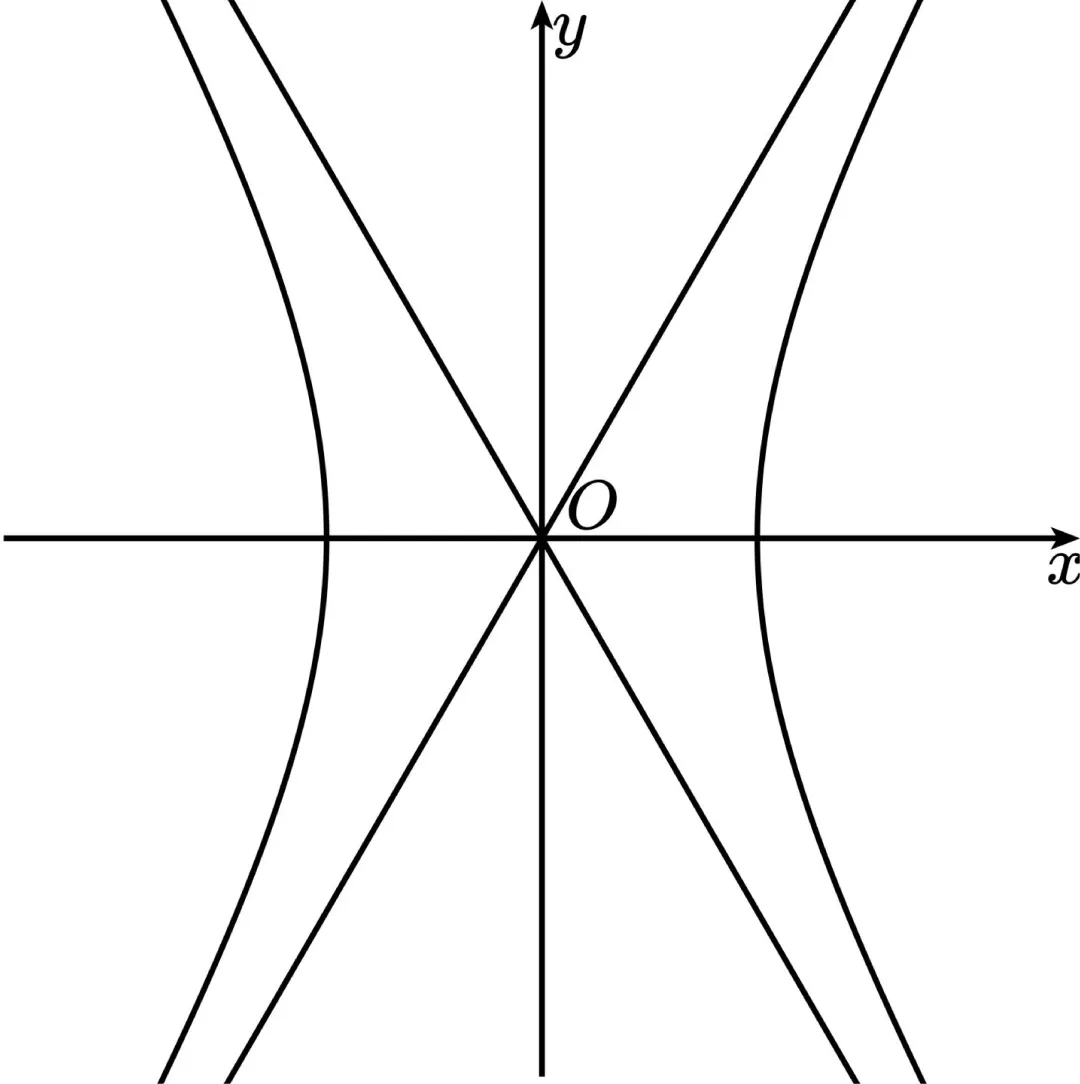
双曲线方程：

法二：同法一

 与  是两条渐近线

逆时针旋转 ，就会回到正常的焦点在 轴的双曲线

设原来  为  上任一点

设旋转后的点为 

记 

设旋转后的点与原点连线倾斜角 

则 ，且 

则 

则 

则

则

，即可证明

.这个数列我们重点关注第三问，它肯定是裂项相消，但是要注意分子的一次函数部分要调整成与分母有关，而且会涉及等比数列的公比。而完成裂项后，求和已经不难搞定了～

25-26高三上·黑龙江哈尔滨·期末

.已知数列为正项数列,.求数列的通项公式;设数列满足, 求数列的通项公式;在的条件下, 设, 求数列的前项和.